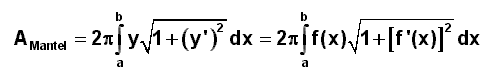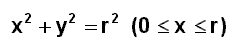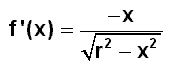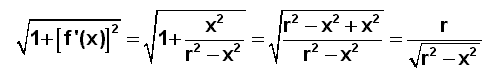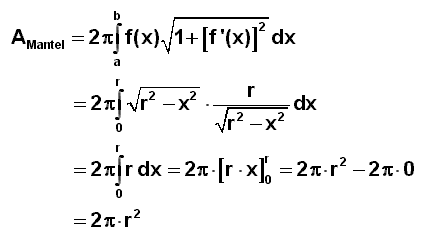Drehkörper - Volumen- und Mantelflächenberechnungen

Baustein 3 - 3(4)

Bestimmung des Mantelflächeninhalts von Rotationskörpern
(nur für Leistungskurse)

3. Berechnung von Beispielproblemen

Berechnungsformel für die Mantelfläche eines Drehkörpers:

BEISPIEL 1: Oberflächeninhalt einer Kugel


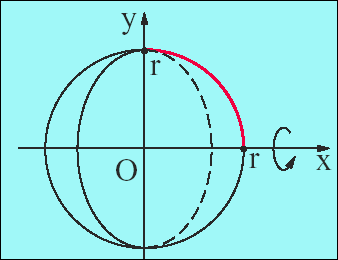
(Bildquelle: TCP 2001, CD zu: Mathematik Gymnasiale Oberstufe. PAETEC-Verlag )

Wir betrachten zunächst eine Halbkugel. Diese wird durch Rotation des Viertelkreises um die x-Achse erzeugt.

Die Funktionsgleichung für den Viertelkreis lautet:

Durch Auflösen nach y folgt:

Mit der Kettenregel ergibt sich als erste Ableitung mit x ¹ r :

Ferner gilt:

Daher ergibt sich in der Berechnungsformel für den Mantelflächeninhalt AMantel für die Halbkugel:

Diesen Wert muss man nun verdoppeln und man erhält den Inhalt der Oberfläche einer Kugel mit Radius r:
   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Seitenanfang Zurück

Weiter
Inhalt Grundlagen Bausteine