Drehkörper - Volumen- und Mantelflächenberechnungen

Baustein 4 - 2(2)

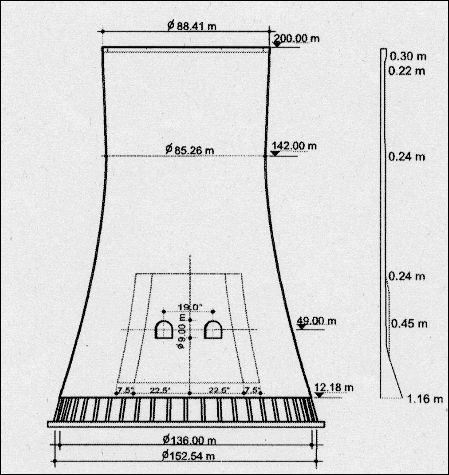
Näherungsweise Bestimmung des Volumens und der Mantelfläche des Kühlturms des 950-MW-BoA-Blocks K des Braunkohlenkraftwerks Niederaußem / NRW

Überlegungen für die Näherungsrechnung

Untenstehend sehen Sie nun eine Querschnittszeichnung des BoA-Kühlturms. Man erkennt, dass alleine die Mantelstützen bereits 12m in die Höhe ragen.
Aus diesem Grund betrachten wir für die nun folgenden näherungsweisen Berechnungen des Kühlturmvolumens den geschlossenen Kühlturmbereich von 12m bis 200m Höhe. Da wir später auch noch die Fläche des Kühlturmmantels berechnen wollen, bietet sich diese Vereinfachung an.

Wir fassen im Folgenden den Kühlturm als einen Drehkörper auf, der durch Rotation des Graphen einer ganzrationalen Funktion f um die x-Achse entsteht. In Wirklichkeit ist der Graph der gesuchten Funktion hyperbelartig und die Drehung erfolgt um die y-Achse. Die exakte Bestimmung übersteigt jedoch die schulischen Möglichkeiten.

Um die ganzrationale Näherungsfunktionfunktion f zu bestimmen, brauchen wir zunächst einige Punkte auf dem Rand des Kühlturms (auf dem Graphen zu f ). Dabei ist zu beachten, dass die berandende Kurve im Innern des Kühlturms sich von der Kurve außen unterscheidet. (Beachten Sie die Dicke der Kühlturmwand in der ersten Skizze rechts.)

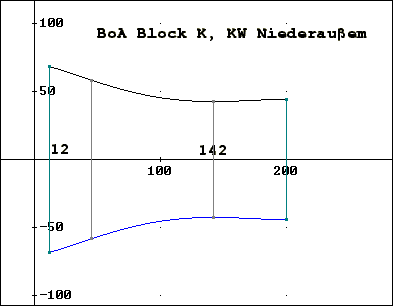
Bestimmung der Außenkurve G des Kühlturms:

Man erkennt (Werte z.T. geschätzt): G(12) » 68,4m, G(45,5) » 58,2m, G(142) » 42,6m, G'(142) = 0 (da in der Höhe von 142m die engste Stelle des Kühlturms vorliegt) und G(200) » 44,2m.

Daher ist der Ansatz einer ganzrationalen Näherungsfunktion 4. Grades notwendig:

G(x) = a·x⁴ + b·x³ + c·x² + d·x + e

DERIVE liefert für die Außenkurve zu G:

Vergleichen Sie hierzu auch den DERIVE-File derive-boa-kraftwerk.dfw !

Bestimmung der Innenkurve K des Kühlturms:

Man erkennt (Werte z.T. geschätzt): K(12) » 67,6m, K(45,5) » 58m, K(142) » 42,5m, K'(142) = 0 (da in der Höhe von 142m die engste Stelle des Kühlturms vorliegt) und K(200) » 44,1m.

Daher ist der Ansatz einer ganzrationalen Näherungsfunktion 4. Grades notwendig:

K(x) = a·x⁴ + b·x³ + c·x² + d·x + e

DERIVE liefert für die Innenkurve zu K:

Vergleichen Sie hierzu auch den DERIVE-File derive-boa-kraftwerk.dfw !

Mittels DERIVE lässt sich nun das Volumen des Kühlturms sowie die Mantelfläche berechnen
(vgl. DERIVE-File derive-boa-kraftwerk.dfw ).

Ergebnisse:
Volumen des Kühlturms (ab 12m Höhe berechnet mit der "Innenkurve" K):

V » 1,453·10⁶ m³ » 1453000 m³

Mantelfläche des Kühlturms (ab 12m Höhe berechnet mit der "Außenkurve" G):

M » 5,931·10⁴ m² » 59310 m²