Drehkörper - Volumen- und Mantelflächenberechnungen |
Baustein 1 - 3(13) |
Was versteht man unter einem "Drehkörper"? |
|
|
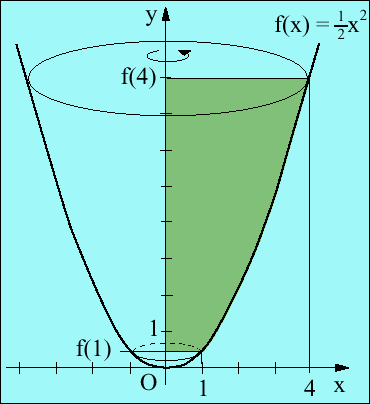
Ein Drehkörper entsteht durch Rotation einer Fläche um eine Rotations- bzw. Drehachse. Jeder Punkt der Außenfläche (Mantel) eines Drehkörpers liegt also auf einer Kreisbahn senkrecht zur Rotationsachse. In der folgenden Abbildung ist die y-Achse die Rotationsachse; die grüne Fläche zwischen dem Graphen zu f (Randfunktion) und der y-Achse ist die rotierende Fläche. Als Rotationskörper entsteht hier ein sogenannter "Paraboloid".
|
|
|
|
|