Die Berechnung der Mantelfläche eines Rotationskörpers bei Drehung um die x-Achse

Es sei f eine über dem Intervall [a ; b] differenzierbare Funktion.
Dann besitzt der Körper, der durch Rotation der Fläche unter dem Graphen der Funktion f über dem Intervall [a ; b] um die x-Achse entsteht, den Mantelflächeninhalt

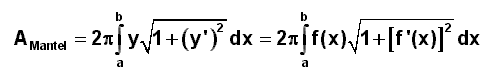
Soll die Oberfläche des Rotationskörpers berechnet werden, so sind die Flächeninhalte der Grundfläche und der Deckfläche zur Mantelfläche zu addieren, falls die erzeugende Kurve nicht mit einer Nullstelle von f beginnt oder endet.

(Dies ist zum Beispiel bei der Berechnung der Kugeloberfläche der Fall.)