Drehkörper - Volumen- und Mantelflächenberechnungen mittels Integralrechnung

Anleitung

Anleitung und Voraussetzungen

Das vorliegende Programm enthält Bausteine zum selbstständigen Lernen im Bereich der Integralrechnung. Das Programm soll erst dann zum Einsatz in einem Selbstlernzentrum kommen, wenn die grundlegenden Methoden der Integralrechnung im Unterricht behandelt worden sind. Insbesondere sollte die Anwendung des Hauptsatzes der Differential- und Integralrechnung den Schülerinnen und Schülern geläufig sein.
Im vorliegenden Selbstlernmaterial geht es um die Bestimmung von Volumen (Rauminhalt) und Mantelfläche von Drehkörpern, die durch Rotation (Drehung) eines Funktionsgraphen einer Funktion f um die x-Achse (oder die y-Achse) entstehen.
Nach einer außermathematischen Einleitung (u. a. Töpfern) und einem "Test zu Drehkörpern" wird zunächst an einer Beispielaufgabe (Kühlturm) die Volumenformel der Integralrechnung hergeleitet (mittels "Scheibenmethode"). Unterstützt wird diese Herleitung durch ein Java-Applet mit dem eine Vielzahl von weiteren Drehkörpern erzeugt werden können.
Um nicht nur innermathematische Anwendungen (z. B. die Herleitung der Volumenformeln für Körper aus der Mittelstufe) zu bearbeiten, sollen Berechnungen für Drehkörper aus unterschiedlichen Bereichen durchgeführt werden, z. B. für zur Zeit Europas höchsten Naturzugkühlturm in Niederaußem / NRW oder für einen Zeppelin (bzw. Cargolifter). Dies erfordert den Einsatz eines Computer-Algebra-Systems (hier: DERIVE für Windows), mit dem zugehörige Funktionsterme (näherungsweise) bestimmt werden können. Ausdrucke (mit Erläuterungen der Befehle) der Derive-Files finden sich in einem eigenen Ordner. Prinzipiell ist aber auch ein anderes CAS-System denkbar, z. B. MuPad oder MathCad.

Bitte maximieren Sie das Fenster, in dem Sie das Selbstlernprogramm anschauen, so dass der gesamte Bildschirm mit dem Fenster ausgefüllt ist. (Falls dies noch nicht so eingestellt ist, klicken Sie rechts oben in der Ecke auf den mittleren Button.) So erhalten Sie optimale Bilder.

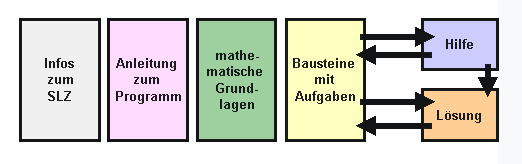
Steuerung

Das Programm ist in unterschiedliche inhaltliche Bereiche unterteilt: Es gibt einerseits die Grundlagen, die die wichtigsten mathematischen Inhalte noch einmal kurz zusammenstellen. Andererseits gibt es die Bausteine, die den zentralen Teil dieses Selbstlernmaterials bilden. Zu den Bausteinen gehören Informationen und Aufgaben, Hilfen und Musterlösungen. Die Steuerung lässt sich entweder über die Navigationsleiste oder über die folgenden Symbole leisten:

Grundlagen zur Integralrechnung	Einen Schritt weiter	Zum Anfang des nächsten Bausteins
Übersicht über die Bausteine	Einen Schritt zurück	Zurück zum Anfang des aktuellen Bausteins
Hilfe zu einer Aufgabe	Musterlösung einer Aufgabe	Weiter gehende Information

Hilfen und Lösungen

Es wird empfohlen, die Aufgaben zunächst von Hand zu lösen und danach mit DERIVE oder unter Verwendung des Java- Applets. Hilfen sollen Sie dabei zunächst unterstützen. Hilfen können den individuellen Fragen nicht immer gerecht werden, manchmal mögen sie zu einfach erscheinen, manchmal vielleicht auch zu schwer. Jedenfalls orientieren sich die Hilfen an den Musterlösungen und enthalten regelmäßig Ausschnitte aus der Gesamtlösung, um auch den etappenartigen Einstieg in eine Aufgabe zu ermöglichen. Hilfen und Lösungen folgen einem Weg, der auch anders oder abgewandelt ausfallen könnte. Auch dies sollte den selbstständig Lernenden nicht irritieren; man kann ja die Lösungen auch dazu nutzen, das Ergebnis eines eigenen Weges gegenzuprüfen.