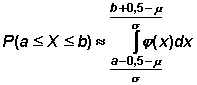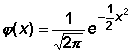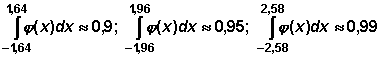Approximation der Binomial- durch die Normalverteilung

Bei großem Stichprobenumfang n fällt die glockenförmige Form der Histogramme von Binomialverteilungen auf. Man kennt diese Form vielleicht aus der Analysis vom Graphen der so genannten GAUSS-Funktion, im Rahmen der Statistik auch Normalverteilung genannt. 

Tatsächlich können für große n die Histogramme durch die "glatte" Normalverteilung so approximiert werden, dass die interessierenden Intervallwahrscheinlichkeiten in guter Näherung statt durch Summation durch eine Integration über die Normalverteilung berechnet werden können.

Genauer gilt die Formel von MOIVRE und LAPLACE:

mit der Gauß-Funktion

Das obige Integral kann man nur numerisch lösen. Die Standardverfahren zur numerischen Integration ergeben dabei folgende Ergebnisse:

Die in der Tabelle aufgeführten Radien, die zum 90%-, 95%- bzw. 99%-Sicherheitsintervall gehören, ergeben sich also (zusammen mit der Näherungsformel von Moivre und Laplace) aus den Eigenschaften der Gauß-Funktion.